ÍNDICE
- Introducción
- 1er caso: Losa Maciza
- 2º caso: Forjado reticular de casetón perdido
Introducción
Al marcar en la planta de una losa maciza o aligerada un punto inicial y final, nos aparece una línea continua en amarillo que une con los dos puntos, dibujando a lo largo de esa línea y, bajo ella, los desplazamientos verticales de todos los puntos, formando una línea más o menos sinuosa en azul que nos mostrará la deformada de esa losa, ya sea para una hipótesis, combinación o la combinación pésima (G+Q) de desplazamientos amplificada.
Cuando vemos en planta la distribución de los soportes o apoyos y marcamos los dos puntos para calcular la flecha, se observa que en las zonas de apoyo aparecen convexidades y, en los centros de vano, concavidades.
Parece sensato que, en un primer vistazo de los isovalores de desplazamientos, estudiemos las gráficas de desplazamientos Z (verticales), pasando por la hipótesis de carga permanente G (que suele representar el porcentaje mayor) y por la hipótesis de sobrecarga de uso Q; para ver a continuación la combinación G+Q y observar dónde se producen los máximos valores, que suelen coincidir con las zonas de mayor concavidad.
En una losa bidireccional no sabemos a priori si la zona de máxima concavidad es la de máxima flecha absoluta, pero lo normal es que lo sea, pues el descenso de apoyos suele ser pequeño, por lo que lo aconsejable es centrarnos en las zonas donde veamos esos máximos. En esos recuadros tampoco tenemos certeza de en qué dirección (X,Y,diagonal) debemos marcar los puntos para obtener la flecha máxima relativa, pero se podría decir que, a la vista de un recuadro de una planta, debería ser en la dirección de la menor distancia entre 2 puntos del perímetro de la concavidad.
Conviene hacerlo así en general.
Si queremos buscar esos bordes del perímetro de la concavidad, puede ser bueno trazar previamente puntos más alejados buscando así su posición.
Pasemos a dar unos ejemplos sencillos para su comprensión con los siguientes datos generales:
- Luz media = 6,50 m
- Vano exterior
- Ley de momentos aproximada
Momento negativo apoyo interior:
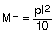
Momento positivo en vano:
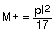
Momento negativo apoyo exterior:
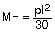
- Tabiquería = 1 kN/m2 ejecutada a los 60 días (2 meses)
- Solado = 1 kN/m2 ejecutado a los 120 días (4 meses)
- Sobrecarga = 2 kN/m2
- Materiales = HA-25 (fck=25 MPa) y B500 (fyk=500 MPa), condiciones medias de temperaturas y humedades en ejecución y vida útil.
1er caso: Losa Maciza
Estimemos un canto de 26 cm, cuya esbeltez es L/h = 650/26 = 25, luego hay que comprobar en principio la flecha, pues para este caso en la tabla 50.2.2.1.a de la EHE-08 el valor de la esbeltez es 23 (para elementos débilmente armados), con lo que hay que justificar su cumplimiento.
Vamos a analizar de forma aproximada una sección de un metro de ancho, tanto para las características de la sección, como para la obtención de los esfuerzos actuantes. Aunque sabemos que la distribución en una losa sobre apoyos aislados no es uniforme, lo haremos así en adelante para simplificar el análisis.
La inercia bruta de la sección de la losa maciza es:
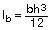
Luego, en nuestro caso:
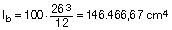
Con este valor se calculan las rigideces en el modelo y se obtienen los desplazamientos elásticos instantáneos que se muestran para cada hipótesis y combinación seleccionada.
Para determinar la flecha entre dos puntos a partir de los desplazamientos, debemos descontar el desplazamiento de los puntos inicial y final.
En la gráfica se muestra una recta que pasa por esos dos puntos (secante) o una tangente al punto inicial (tangente), dependiendo de la selección realizada. Respecto a esa recta se mide la flecha.
Los valores que se muestran son:
- Luz del vano L
- Flecha absoluta
- Flecha relativa respecto a L (secante) o 2L (tangente)
- Combinación pésima G+Q obtenida a partir de las combinaciones de “Desplazamientos” seleccionados en los datos generales de la obra. Se consideran sólo las hipótesis de origen gravitatorio G y Q (activado por defecto). También se puede seleccionar por hipótesis o combinación.
Vemos que se muestra un valor de “Amplificación de los desplazamientos” = 2,5 (valor por defecto), que hace exactamente lo que dice: multiplicar por ese valor los desplazamientos de las hipótesis de desplazamientos para mostrar los resultados.
Este factor amplificador se ha de incorporar y tener en cuenta todos los parámetros relativos a:
- Plazo de desencofrado
- Proceso constructivo
- Fenómenos térmicos
- Fenómenos reológicos (fluencia, retracción)
Admitimos que, a partir de la flecha elástica instantánea, es posible obtener la flecha total o la flecha activa (posterior a la construcción de los elementos dañables, por ejemplo, tabiquería o pavimentos rígidos sin juntas), basándonos en la estimación de los parámetros citados anteriormente. Colocando el valor adecuado obtendremos el resultado de la flecha que estemos buscando para comparar con los límites normativos.
Supongamos un proceso constructivo habitual, con sus cargas de edificación:
- Peso propio losa (h=26 cm) = 6,5 kN/m2 descimbrada a los 28 días (1 mes)
Con las leyes de un vano exterior (como si aplicáramos pórticos virtuales), determinamos la ley de momentos y la armadura necesaria por metro de ancho.
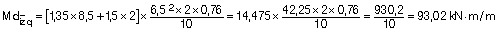
Que obtendríamos de forma aproximada:
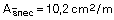
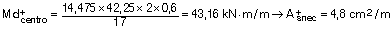
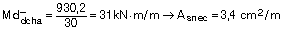

Calculamos el momento fisuración:
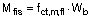
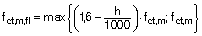
Siendo fct,m,fl: la resistencia media del hormigón a flexotracción
fct,m: la resistencia media del hormigón a tracción
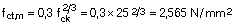
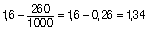
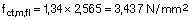
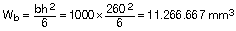
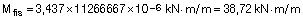
Quedamos del lado de la seguridad considerando los momentos de servicio debido a la carga total:
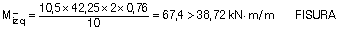
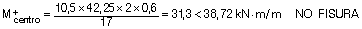
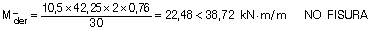
Determinando la inercia fisurada Ifis y la inercia equivalente Ie de Branson:
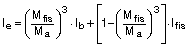
donde:
Ie: inercia equivalente
Mfis: momento de fisuración
Ma: momento actuante en la sección
Ib: inercia bruta
Ifis: inercia fisurada
Esto lo haremos en las 3 secciones en estudio:
Y determinamos la inercia media equivalente del tramo:
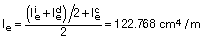
Siendo:
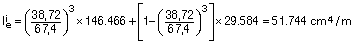
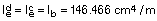
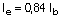
De forma conservadora, reducimos la inercia equivalente a:
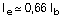
Al resultado de las flechas elásticas dadas por el programa deberíamos aplicarle un coeficiente corrector debido a la fisuración de las secciones que llamaremos Ke, y cuyo valor sería:
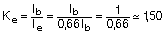
Si aplicamos el método de la EHE-08 (similar a ACI-08), en el que suponemos que la flecha diferida es proporcional a la flecha instantánea por un factor λ cuyo valor es:
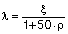
ξ: coeficiente en función del tiempo o duración de la carga
r: cuantía media de armadura comprimida
Si en la losa colocamos un mallazo superior e inferior que nos cubra por ejemplo el 1‰ (r = 0,001), ξ tomaría los siguientes valores:
| t | ξ |
|---|---|
| ∞ ≥ 5 años | 2,0 |
| 1 año | 1,4 |
| 6 meses | 1,2 |
| 1 mes | 0,7 |
| 2 semanas | 0,5 |
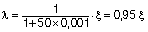
Veamos el proceso constructivo y las flechas que se producen.
Supongamos en primer lugar la flecha total:
| Carga permanente | Valor (kN/m2) | t (días) | ξ |
|---|---|---|---|
| Peso propio | 6,5 | 28 | 2-0,7 = 1,3 |
| Tabiquería | 1,0 | 60 | 2-0,8 = 1,2 |
| Solado | 1,0 | 120 | 2-1 = 1 |
| Sobrecarga de uso | 2 | 365 | 2-1,4 = 0,6 |
ξ = ξ (∞) - ξ (t)
t: cuando entre en carga
Con sobrecarga de uso supuesta sólo la parte cuasi permanente produce flecha diferida (para viviendas ψ2=0,3) tendríamos aplicándolo en el total:
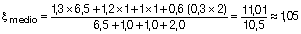
Luego:
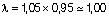
Para obtener la flecha instantánea corregida por la reducción de inercia debida a la fisuración, al valor de la flecha instantánea fi lo multiplicamos por Ke:
finst = Ke · fi = 1,50 fi
Por otra parte, la flecha diferida total hemos obtenido un coeficiente l = 1,00, luego
fdif = λ · finst = 1,00 · finst
y la flecha total es:
fTotal = finst + fdif = 1,5 fi + 1,00 x 1,5 fi = 3,00 fi
Este valor 3,00 es precisamente ese coeficiente que se presenta como “Amplificación de los desplazamientos” (y que por defecto es 2,5)
En la memoria de cálculo de CYPECAD se menciona que su valor puede estar comprendido entre 2,5 y 3,0 según el proceso constructivo.
En este ejemplo hemos visto que el valor es 3,00, cantidad que introduciríamos en la casilla para consultar la flecha total, y ver los resultados seleccionados entre dos puntos.
Análogamente, si quisiéramos determinar la flecha activa, en este caso, la que se produce con posterioridad a la construcción del elemento dañable, deberíamos quitar la que se produce antes de su construcción. Para ello, y en este ejemplo, debemos quitar la flecha instantánea debida al peso propio del forjado y la diferida desde que se descimbró hasta la construcción de la tabiquería a los 60 días, luego ξp.propio = (2- 0,8) = 1,2, y quedaría:
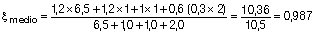
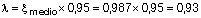
Por consiguiente la flecha diferida será fdif = 0,93 finst.
En cuanto a la flecha instantánea a considerar hemos de quitar la parte correspondiente debida al peso propio. Luego por proporcionalidad de las cargas sin el peso propio a las totales:
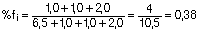
Resultando
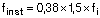
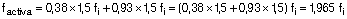
Este valor sería el que tendría que introducir en la casilla de “Amplificación de los desplazamientos” para obtener la flecha activa.
Evidentemente hemos visto que para las cargas previstas y plazos de ejecución, redondeando a valores enteros, podemos estimar que una losa maciza tiene una flecha activa del orden de 2,0 veces la flecha elástica instantánea determinada con la sección bruta, y una flecha total del orden de 3,0 veces esa flecha instantánea de forma aproximada.
2º caso: Forjado reticular de casetón perdido
A continuación, haremos una estimación similar para un forjado reticular introducido con CYPECAD.
Sea un forjado reticular de casetón perdido con la siguiente geometría:
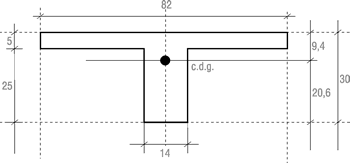
Determinamos el centro de gravedad de la sección y respecto a éste la inercia de la sección bruta, obteniendo:
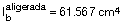
Si hacemos lo mismo en la zona de ábacos, que sería como una losa maciza de 30 cm de canto y 82 cm de ancho:
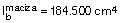
La inercia promediada de la sección a lo largo del tramo, podríamos estimarla como:
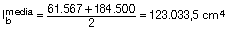
En el modelo de CYPECAD, la inercia aplicada a toda la malla del paño de cualquier reticular, ya sea en zona aligerada o maciza, es la misma y se toma igual a la mitad de la zona maciza, que en este caso sería:
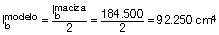
y con esta inercia se determinan los desplazamientos elásticos para cada hipótesis.
Ahora procedería verificar si con los esfuerzos actuantes las secciones se fisuran o no, y determinar la inercia equivalente.
En la sección maciza y tomando ancho = 0,82 m, el momento de fisuración es:
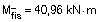
y en la zona aligerada:
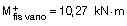
Estimamos los momentos actuantes:
| Peso propio forjado: | 4,6 kN/m2 | (*) |
| Tabiquería: | 1,0 kN/m2 | |
| Solados: | 1,0 kN/m2 | |
| Sobrecarga de uso: | 2,0 kN/m28,6 kN/m2 |
(*) Se ha tomado el de la zona aligerada, dado que la zona maciza influye poco en los momentos actuantes.
Estimamos los momentos por nervio en una hipotética banda de soportes:
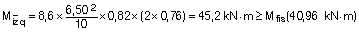
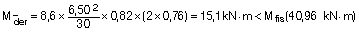
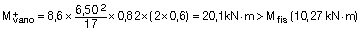
Se observa que en negativos apenas fisura, pero sí lo hace en la zona de positivos en vano.
Estimando la inercia equivalente en vano:
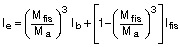
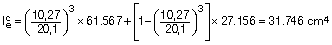
En apoyo derecho, la tomaremos igual a la bruta aproximadamente:
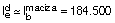
Y en el apoyo izquierdo, se obtiene:
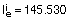
Promediando:
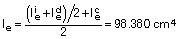
La inercia considerada en el cálculo es la siguiente:
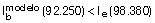
Por ello, no aplicaremos ninguna corrección por este aspecto, aunque para mayor seguridad, tomaremos:

Amplificando además por:
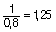
En cuanto a:
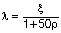
Tomaremos del lado de la seguridad que ρ = 0, luego λ = ξ, y el mismo proceso constructivo y plazos, luego:
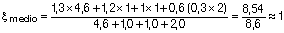
podemos decir que la flecha diferida es aproximadamente igual a la flecha instantánea (fdif ≈ finst = 1,25 fi); y que la flecha total resulta:
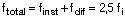
Ya que finst = 1,25 fi
Ahora vamos a obtener la flecha diferida con posterioridad a la construcción de los tabiques:
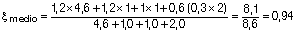
y debemos dejar la flecha instantánea sin el peso propio del forjado:
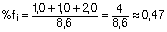
luego la flecha activa será:
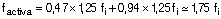
Podemos decir que la flecha total a plazo infinito en un reticular debe obtenerse con un coeficiente de amplificación de los desplazamientos del orden de 2,5 la flecha elástica instantánea del programa, y que para la flecha activa habría que multiplicar por 1,75 la flecha elástica instantánea.
Hay que tener en cuenta que los coeficientes indicados son de aplicación para casos habituales de edificación tales como los mencionados, en cuanto a luces, cantos, cargas, proceso constructivo y condiciones ambientales normales, y plazos de descimbrado y entrada de las diferentes fracciones de las cargas a lo largo del tiempo.
Si se varían dichas condiciones, lógicamente habría que aplicar los coeficientes correctores pertinentes.
Si queremos verificar la flecha debida al confort, será suficiente con analizar la flecha debida a la sobrecarga de uso, en la hipótesis Q.
CUADRO RESUMEN
| Garantiza | Flecha | Amplificación | FORJADO | COMBINACIÓN |
| INTEGRIDAD | ACTIVA | 2,00 | LOSA MACIZA | G+Q Pésima |
| INTEGRIDAD | ACTIVA | 1,75 | RETICULAR | G+Q Pésima |
| APARIENCIA | TOTAL PLAZO INF. | 3,00 | LOSA MACIZA | G+Q Pésima |
| APARIENCIA | TOTAL PLAZO INF. | 2,50 | RETICULAR | G+Q Pésima |
| CONFORT | INSTANTÁNEA DE SOBRECARGA | 1,50 | LOSA MACIZA | Hipótesis Q |
| CONFORT | INSTANTÁNEA DE SOBRECARGA | 1,25 | RETICULAR | Hipótesis Q |



